首发于SDNLAB网站,链接:https://www.sdnlab.com/23953.html
IBN(基于意图的网络)是近年来网络领域中最热门的话题之一,网络验证是其中最关键的环节。我们在此之前一直专注于网络配置的自动化,例如根据模板创建配置进行编排并在网络上部署,这确实可以有效的减少人为上操作错误。但是随着网络基础设施变得越来越复杂,网络规模也越来越大,验证是否能够达到预期结果也至关重要。对网络验证领域的研究最早是在学术研究实验室,比如卡梅隆大学,AT&T实验室,斯坦福大学和微软研究院。该技术的灵感来自计算机科学领域,即形式化验证,基于严格的数学表述和模型去验证网络中的问题。
维基百科对形式化验证的解释是这样的: 在计算机硬件(特别是集成电路)和软件系统的设计过程中,形式化验证的含义是根据某个或某些形式化规范或属性,使用数学的方法证明其正确性或非正确性。 在芯片设计领域中,最知名的失败案例,是Intel的Pentium处理器浮点运算单元出错(FDIV Bug),数以万计的Pentium处理器不得不回收和替换,给Intel造成了约4.7亿美元的损失。在那之后,Intel开始在其芯片设计中广泛采用形式化验证。除了在芯片领域,形式化验证还在许多领域中应用,例如航天,操作系统,金融领域等等。
无论是硬件还是软件工程,归根结底是数学问题。如果我们可以验证软件,为什么不验证网络?从某种意义上说,网络就像软件一样,可以对不同网络层进行抽象建模。它接受输入,例如网络配置,拓扑,路由表,数据包起始位置等等,并根据这些输入逐步执行操作,例如使用转发规则,如果数据包的IP目的地址是10.2.1.0/24,然后将其发送到指定的出接口。最后计算出验证结果,例如数据包被丢弃,修改,转发到指定出接口。
下文将介绍形式化验证在网络领域中的应用,主要分为四个小节:
- 模型检查(Model Checking)
- 定理证明(Theorem Proving)
- 符号执行(Symbolic Execution)
- SAT/SMT求解器(SAT/SMT Solvers)
模型检查(Model Checking)
模型检查(Model Checking)是一种基于状态迁移系统的自动验证技术。它最早是由Clarke和他的研究生Emerson以及Sistla在1981年提出来的,基本想法是将系统建构为一个有限状态机(Finite State Machine),通过有效的搜索方法(状态空间检索state-space search)来检查给定的系统是否满足规范,检查系统是否满足所需的不变式。它将转换模型系统分解成逻辑公式,然后计算出能够满足公式的条件。当检查出不满足时,会返回一个反例可以帮助人们去解决这个系统的问题。由于模型检查的工作机制会导致系统状态空间的大小呈指数增长,存在状态空间爆炸的问题。因此学术界和业界提出了许多优化的方法,例如:
- 有界模型检查(Bounded Model Checking),使用SAT(Boolean satisfiability)求解器在一定边界条件下寻找反例。
- 符号模型检查(Symbolic Model Checking),使用二元决策图(Binary Decision Diagrams)而非独立的状态列表来表达状态空间。进一步简化的有序二元决策图(Reduced Ordered Binary Decision Diagrams),可以缓解状态爆炸问题。
- 延伸阅读:二元决策图基础
模型检查在网络领域中的应用,例如Flowchecker使用二进制决策图(BDD)根据openflow控制器转发行为构建状态机,然后使用符号模型检查工具NuSMV检测网络配置错误。当数据包从服务器A发往服务器B时,每个网络中的设备可以在特定接口上转发数据包,丢弃包,或修改包头并转发。
以下图为例,交换机SA有一些转发表,例如规则RA1将目的IP是192.168.1.0/24网段的报文通过接口pa0发出去。网络系统的状态(State)由数据包头空间p以及所在位置l决定,例如初始状态数据包是一个全空间(表示所有的报文),对应的位置是主机PA,那么初始状态(Initial State)可以编码为(p, PA)。交换机上在接口之间转发数据包的规则可以被认为是状态转换(State Transitions),例如(p, SA) → (p′, SB) (p.dst ∈ 192.168.2.024 & p.dst′ = p.dst)表示SA设备上RA2的转发逻辑。
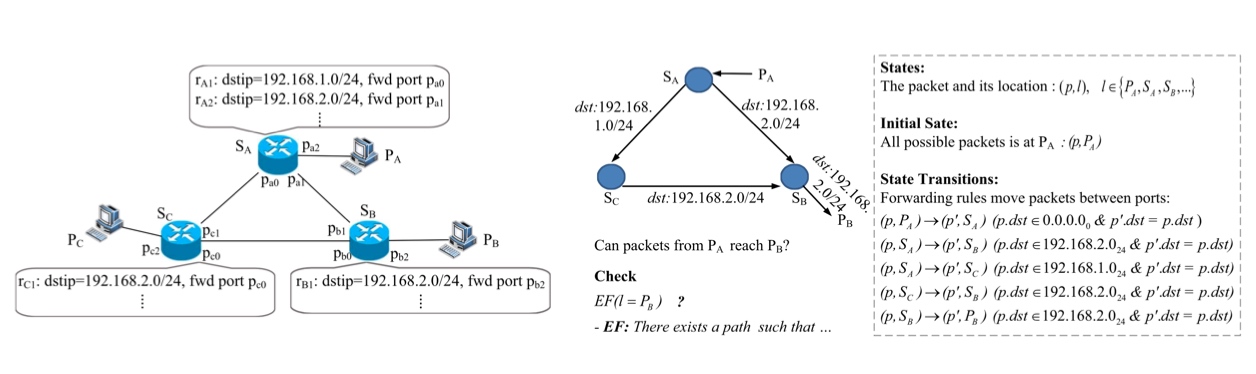
当对报文初始状态以及状态之间的转换编码完成后,可以定义属性(property),例如查看是否存在一个报文可以从主机PA转发到主机PB上。在CTL的语法中,从PA到PB的值可以表示为EF(l=PB),可以输入模型和属性到模型检查器引擎(例如NuSMV)。如果引擎返回pass,该属性保留在系统模型上。如果模型不满足该属性,系统将返回一个反例。上面的例子中,模型满足输入的属性。
定理证明(Theorem Proving)
定理证明是另一个重要的形式验证方法。它对系统用严格语义的数学符号进行描述和推理,将模型抽象为逻辑公式,然后使用自动的逻辑推理技术去验证。针对不同的应用领域,运用不同的形式演算方法,出现了多种定理证明系统,主要分为交互式定理证明器(interactive theorem prover)和自动化定理证明器(automated theorem prover)两大类。交互式定理证明器以人机交互为基础,使用者先指定每一个证明步骤所需要做的工作,然后由计算机完成具体的工作细节。因此对用户而言十分复杂,而且并没有办法确保事先人为制定的规则和定理的正确性,因此最终的正确性也值得怀疑,即前提若有错误,则最终的验证结果就不一定正确。与模型检查不同,定理证明没有状态的概念,不需要对系统的状态空间建模。通常用户使用定理证明作为主要验证,以避免状态爆炸问题。
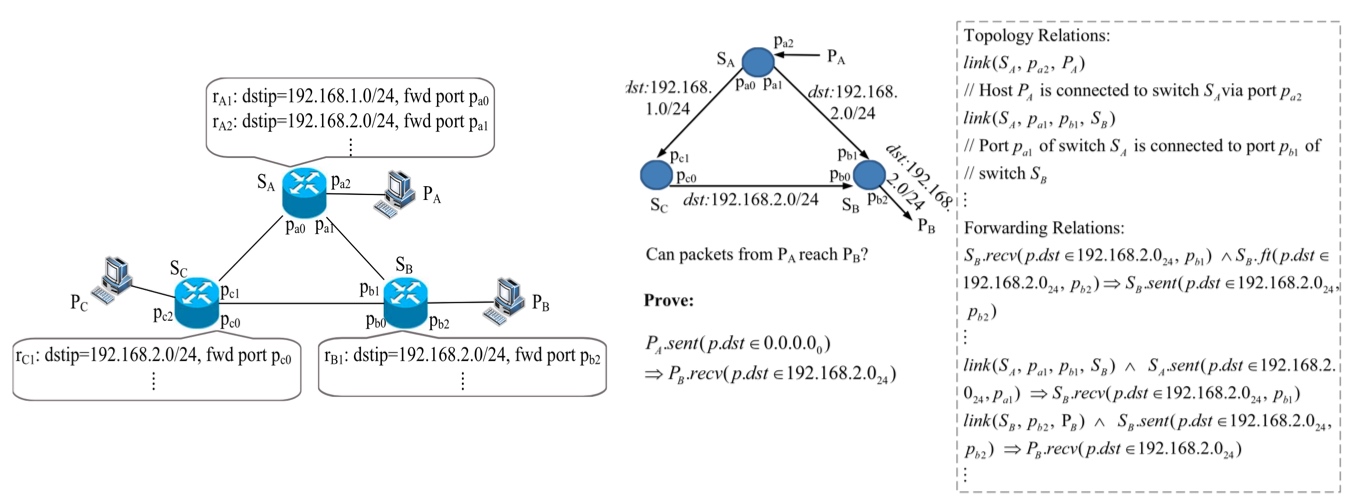
定理证明在网络领域中的应用,例如VeriCon验证无限状态SDN程序。以下图为例,输入网络拓扑,例如(SA,pa1,pb1,SB)可以表示为交换机SA接口pa1连接到交换机SB接口SB。输入转发规则,例如SB.recv(p.dst∈192.168.2.0/24,pb1)表示目的IP为192.168.2.0/24数据包p可以在交换机SB的接口pb1接受。判断是否来自PA的数据包可以到达PB。当查看报文能否从主机PA转发到主机PB上,我们可以证明PAsent(p.dst∈0.0.0.0/0)=>PB.recv(p.dst∈192.168.2.0/24)公式为true。值得一提的是,当不满足公式时,定理证明不能提供反例,所以用户没办法依据反例进行分析和调试。
符号执行(Symbolic Execution)
维基百科对符号执行的解释是这样的: 符号执行是一种程序分析技术。其可以通过分析程序来得到让特定代码区域执行的输入。使用符号执行分析一个程序时,该程序会使用符号值作为输入,而非一般执行程序时使用的具体值。在达到目标代码时,分析器可以得到相应的路径约束,然后通过约束求解器来得到可以触发目标代码的具体值。
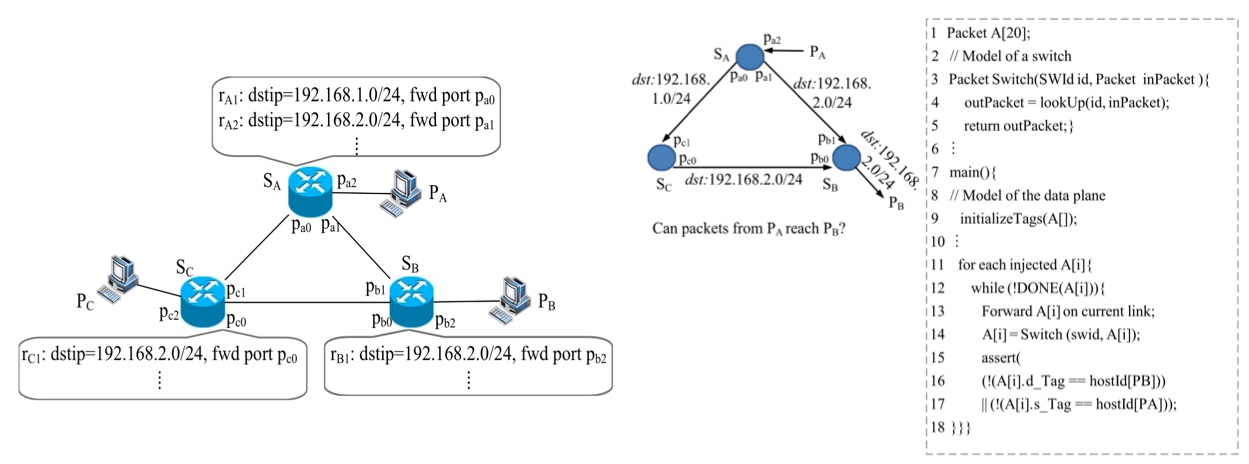
符号执行技术是一种白盒的静态分析技术。从表面上看,网络与软件代码有些不同,网络包括路由器,网卡,线缆等。整个网络也可以被视为”程序“,例如路由器的转发表可以被认为是一条程序语句表示转发特定的报文到出接口。在网络领域中,应用符号执行技术项目有HSA,SymNet等等。那么如何形式化地表示符号执行的过程呢?程序的所有执行路径可以表示为树,叫做执行树。每一个条件分支都会产生两个不同约束,符号执行要探索的执行路径按照指数增长。以下图为例,该程序段表示了转发规则如何在设备接口之间转发报文。每次迭代(第12行)都会处理一个报文,分为两个步骤:1. 转发数据包到当前链路。2. 然后将其作为参数转发到于此链路相连的设备上。我们可以定义一个断言声明:定义从主机PA的数据包转发到主机PB,A[i].s_Tag表示原始报文,A[i].d_Tag表示当前位置上的报文。我们将程序和断言输入到符号执行引擎。该引擎输入一个符号值表示报文,然后分析程序的执行路径,最终会返回断言是否成立。
SAT/SMT求解器(SAT/SMT Solvers)
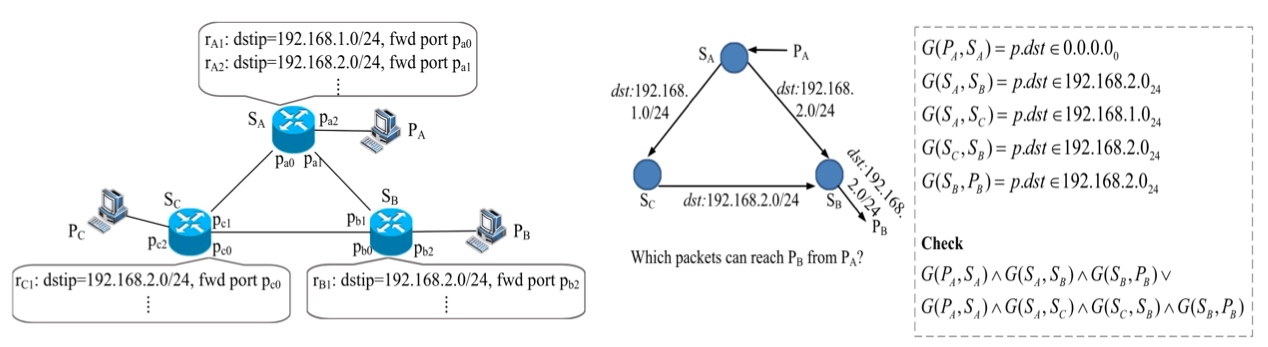
SAT求解器采用基于David-Putnam的搜索技术(也称DP方法)解决逻辑公式的可满足性问题。SMT起源于对SAT的扩充。SAT的表达能力有很大的局限性, 许多问题需要用更强大的逻辑来表达。如果给定一个公式,如果存在一个赋值使该公式为真,那么称该公式是可满足的,否则称该公式是不可满足的。SAT求解器的输入用逻辑表达的公式,求解器自动决定相应内容是否可满足。以下图为例,对设备转发表进行编码G(SA,SB)=p.dst∈192.168.2/24是一个布尔公式,表示为设备SA到设备SB之间数据报文转发的约束。如果想验证报文从主机PA是否能到主机PB,将两条路径PA→SA→SB→PB和PA→SA→SC→SB→PB的逻辑表达的公式输入到求解器中进行运算,如果不满足会输出一个反例。
SAT/SMT求解器大量的应用在网络验证中,AWS有一个ARG(Automated Reasoning Group)团队,他们借助自动推理技术检测可能潜在暴露脆弱数据的各类配置错误。例如Zelkova策略分析引擎可以自动检测各种类别的资源配置错误,它翻译策略成SMT约束公式,然后使用Z3,Z3AUTOMATA和CVC4求解器进行证明是否能够满足Ture,或者返回一个反例满足为False。当用户下发这个策略后,S3会对这个bucket打上public标签提醒用户,这是怎么做到的呢?Zelkova翻译用户的策略转换为数学公式,仅当其左侧和右侧均为真时才为真。Resource和Principal是变量,就像在代数中使用x和y一样。
(Resource = “arn:aws:s3:::test-bucket”) ∧ (Principal ≠ 11112222333)
下一步是要确定此策略公式是否允许公共访问,Zelkova通过对比两个策略决定哪个策略更宽松(permissive)。Zelkova具有一项特殊的策略,该策略允许未经授权的匿名用户访问S3资源。Zelkova将用户下发的策略与此策略进行比较。如果用户的政策更为宽松(permissive),则表明政策允许公共访问。如果用户的策略严格限制访问,例如基于源VPC endpoint(aws:SourceVpce)或源IP地址(aws:SourceIp),那么用户的策略就不会比这个特殊策略更为宽松,因此Zelkova认为用户的策略不允许公共访问。延伸阅读:AWS基于模型的网络验证
参考文献